 |
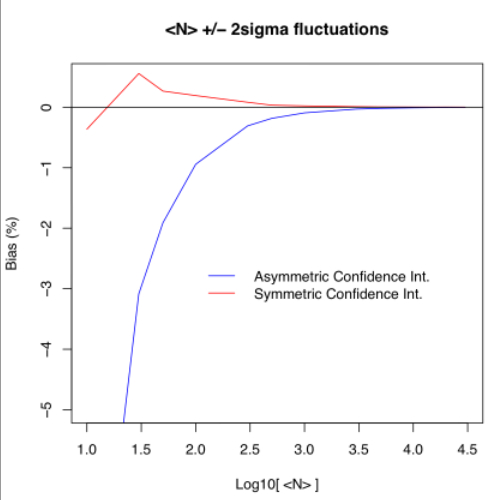
| Figure 1 - Bias (in percent) as a function of assumed input expectation value (mean count) for 2-sigma fluctuations: asymmetric (blue) and symmetric (red) confidence intervals. Click to enlarge. |
F. Masci, 4 February 2008
We have simulated the bias from inverse-variance weighted averaging of purely Poisson distributed measurements where the variances σ2i are derived from the measurements xi, i.e., σ2i = xi. Results are summarized in Tables 1 & 2 for different sigma limits and whether the confidence interval (total probability) about the assumed mean is symmetric or asymmetric.
The measurements may represent the number of photo-electrons recorded at a pixel in an imaging detector. It's important to note that the biases computed below are for pure Poisson fluctuations. Other contributions to the measurement variance such as detector read-noise, which is likely to be independent and Gaussian in nature, will dilute the bias from inverse Poisson-variance weighting. Furthermore, artificial pixel responsivity variations must be corrected before computing any inverse-variance weighted average using Poisson derived variances.
Table 1 summarizes results for the bias in the inverse Poisson-variance weighted average with the confidence interval (integrated probability) kept asymmetric about the mean μ (truth). This is due to the non-zero skewness in the Poisson distribution where the skew scales as μ-1/2. This case may be encountered when one blindly uses the same number of standard deviations about the mean for retaining data after outlier rejection, i.e., within μ ± nσ, where σ = μ1/2 for Poisson-distributed data. This ignores the possibility that the underlying distribution of the population is asymmetric, e.g., as in the Poisson regime.
We have simulated this scenario by randomly drawing 10,000,000 samples
from a Poisson distribution with assumed mean μ (column 1) and
then retaining only values xi within
μ ± 2σ and μ ± 3σ.
These values were then combined to compute an inverse Poisson-variance weighted
average (column 2):
Weighted Avg = ∑i(xi/σ2i) / ∑i(1/σ2i) = ∑i(xi/xi) / ∑i(1/xi) = Ns / ∑i(1/xi),
where Ns = sample size.
The bias in the weighted average (column 3)
is measured relative to the true mean μ:
Bias (%) = 100 * (Weighted Avg - μ) / μ.
μ (truth) | Weighted Avg | Bias (%) | n in ±nσ
---------------------------------------------------------
10 8.963957 -10.360428 2.000
30 29.074249 -3.085837 2.000
50 49.045239 -1.909521 2.000
100 99.056126 -0.943874 2.000
300 299.076390 -0.307870 2.000
500 499.070494 -0.185901 2.000
1000 999.063474 -0.093653 2.000
3000 2999.059874 -0.031338 2.000
5000 4999.058573 -0.018829 2.000
10000 9999.108676 -0.008913 2.000
15000 14999.109218 -0.005939 2.000
20000 19999.021523 -0.004892 2.000
30000 29999.093535 -0.003022 2.000
.....................................................
10 8.830797 -11.692025 3.000
30 28.948477 -3.505076 3.000
50 48.964837 -2.070327 3.000
100 98.973086 -1.026914 3.000
300 298.990371 -0.336543 3.000
500 498.981064 -0.203787 3.000
1000 998.997981 -0.100202 3.000
3000 2998.983203 -0.033893 3.000
5000 4998.994062 -0.020119 3.000
10000 9998.955520 -0.010445 3.000
15000 14998.989938 -0.006734 3.000
20000 19999.000118 -0.004999 3.000
30000 29999.022856 -0.003257 3.000
---------------------------------------------------------
Table 1 - Results for bias in inverse-variance weighted
average assuming asymmetric (unbalanced)
confidence intervals about the mean.
Table 2 summarizes results for the bias in the inverse Poisson-variance
weighted
average with the confidence interval (integrated probability) made symmetric
about the mean (truth).
This is done by first fixing an
upper threshold nU, then finding the lower
threshold nL such that:
Prob[ μ - nLσ < xi < μ ] = Prob[ μ < xi < μ + nUσ ].
10,000,000 random draws were initially made. Then only those values
xi within the new interval
μ - nLσ to μ + nUσ
were used for the weighted averaging (column 2).
All other columns are the same as defined for Table 1 above.
μ (truth) | Weighted Avg | Bias (%) | nL | nU
-----------------------------------------------------------------
10 9.962058 -0.379419 0.949 2.000
30 30.165960 0.553199 1.095 2.000
50 50.132571 0.265143 1.273 2.000
100 100.198941 0.198941 1.400 2.000
300 300.255111 0.085037 1.559 2.000
500 500.158431 0.031686 1.655 2.000
1000 1000.203027 0.020303 1.739 2.000
3000 3000.253909 0.008464 1.826 2.000
5000 5000.205662 0.004113 1.867 2.000
10000 10000.167745 0.001677 1.910 2.000
15000 15000.138307 0.000922 1.919 2.000
20000 20000.289366 0.001447 1.923 2.000
30000 30000.361102 0.001204 1.940 2.000
.............................................................
10 10.083210 0.832102 0.949 3.000
30 30.101412 0.338040 1.278 3.000
50 50.127484 0.254967 1.414 3.000
100 100.137742 0.137742 1.600 3.000
300 300.190409 0.063470 1.848 3.000
500 500.334528 0.066906 1.923 3.000
1000 1000.379039 0.037904 2.055 3.000
3000 3000.423075 0.014102 2.264 3.000
5000 5000.400008 0.008000 2.362 3.000
10000 10000.478232 0.004782 2.460 3.000
15000 15000.419536 0.002797 2.523 3.000
20000 20000.534468 0.002672 2.560 3.000
30000 30000.448127 0.001494 2.610 3.000
-----------------------------------------------------------------
Table 2 - Results for bias in inverse-variance weighted average
assuming symmetric (balanced) confidence intervals
about the mean.
 |
| Figure 1 - Bias (in percent) as a function of assumed input expectation value (mean count) for 2-sigma fluctuations: asymmetric (blue) and symmetric (red) confidence intervals. Click to enlarge. |
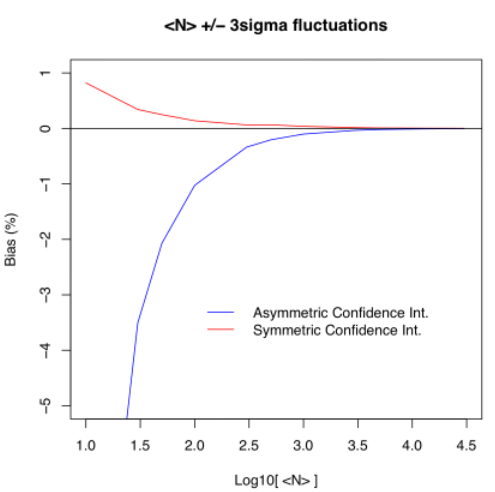 |
| Figure 2 - Bias (in percent) as a function of assumed input expectation value (mean count) for 3-sigma fluctuations: asymmetric (blue) and symmetric (red) confidence intervals. Click to enlarge. |
The above simulations were generated using the S-Plus/R Code:
PoissonBias.r