Deconvolution of WIRE Primary Survey Data



Contents
1. Overview
2. Richardson-Lucy and other Fourier-Based Algorithms
2.2  Richardson-Lucy and the UltraDeep Survey
3. CLEAN
4. For additional reading, try Appendix B of my thesis.


1. Overview

The WIRE PSF is fairly broad, and as a result the deep surveys are expected to be confusion limited. Ideally, one would like to decrease this confusion by increasing the spatial resolution of the data. Like all imaging data, the observed WIRE PSF is a convolution of the true luminosity distribution with the telescope optical transfer function, the pixels of the imaging array, jitter in the spacecraft, etc. In principle, given a known point spread function it is possible to invert the convolution and recover the truth image. In reality this is fairly difficult due to the limited number of spatial frequencies sampled by a real, pixellated image of finite extent and the limited S/N in the image. As a result, all deconvolution algorithms make additional assumptions about the data in an attempt to constrain their solutions, and one must choose an algorithm that is appropriate for the data and what one wants to extract from it.

There are two important facets of the WIRE survey data that dictate the applicability (or lack thereof) of deconvolution:



This first point is of the greatest importance. An algorithm which achieves high S/N at the expense of low flux features will not be acceptable. The second point is relevant in that point sources are the hardest objects for deconvolution algorithms to reproduce accurately, since they require knowledge of spatial frequencies higher (well, infinite for a true point source) than can be sampled.

2. Richardson-Lucy and other Fourier algorithms

The Richardson-Lucy maximum likelihood algorithm is the most common in use and has been successfully applied to a wide variety of data. A simulated coadded 12um image from the data pipeline was used for testing. A PSF was derived from the 10 or so brightest stars without bright nearby neighbors in the coadded image using DAOPHOT. The LUCY task in STSDAS was then applied.

Truth Image Raw Coadd Lucy
Truth Image Pipeline Coadder R-L 20 iterations


The achieved spatial resolution for the bright stars is about 11", close to the diffraction limit. The Gibbs ringing around the bright stars is immediately apparent. Note the extremely mottled appearance of the background due to noise amplification. Both this and the ringing are artifacts common to all fourier-based algorithms. The noise amplification is a result the initial iterations correlating all of the pixels on the size scale of the PSF. Afterwards, high-sigma noise outliers get built up iteratively as if they were real sources. Thus, while the increased spatial resolution should in theory decrease the confusion problem, it only does so for the brightest sources, which weren't confused anyway. In reality, the deconvolution process actually increases the confusion of faint sources due to noise amplification. Results for Maximum Entropy are similar.

Another interesting algorithm is the Lucy-Hook coaddition and deconvolution algorithm, which is designed specifically for undersampled, sub-pixel dithered images. Unfortunately, it is extremely computer intensive, and I am having trouble finding an IPAC computer up to the task of coadding 40 frames. I will have results shortly as soon as I can ship the data to a UH-IfA machine with a gig of ram. In the meanwhile, here is a coadd of 8 frames:

Lucy-Hook
Lucy-Hook Coaddition of 8 12um Frames


Obviously, since this algorithm is the R-L code at heart, it suffers many of the same problems. It is likely that these techniques may be most useful for the AI programs, where S/N will be much higher.

2.2. R-L and the UltraDeep Survey

Because the ultradeep survey is expected to be confusion-limited with high S/N, photometric noise should not be such a serious problem as in the shorter surveys, i.e. most of observed flux is real, and not poisson noise spikes. As a result, there should be far less noise amplification with a corresponding increase in reliability.

The deconvolution experiment was done in the usual fashion. A simulated ultradeep coadd at 25 microns was acquired from Dave Shupe. A new PSF was extracted directly from this coadd using DAOPHOT. The background pedestal value was added back into the coadd since R-L since negative flux is non- physical and R-L is unforgiving of such things. The R-L algorithm was iterated 20 times. A new PSF was extracted from the deconvolved image using DAOPHOT; this PSF was then used as the template for the source extractor. Sources were extracted by running all the separate parts of WIREDAO by hand. The output from these tasks were then processed using MATCH and STAT.

The results indicate an increase of 80% in the number of true point sources detected, with a very high degree of reliability. A graphical comparison of the output of MATCH is included here. The raw coadd is on the left (8000) and the deconvolved coadd is on the right (8001). It appears that sources can be extracted with greater than 95% reliability down to a flux level of just over 0.1 mJy.

There are still a number of sources of concern. The first, which has been mostly resolved, is due to the observed notch in the differential completeness in both the raw and deconvolved coadds.. This is particularly surprising, since one doesn't expect a drop in reliability for such bright sources. An examination of the false detected sources, however, reveals the problem: artifacting around very bright point sources. Elimination of these artifacts greatly improves reliability. Ultimately, this should be characterized and the final WIRE source list should be processed to eliminate these false sources, since they will be predictable.

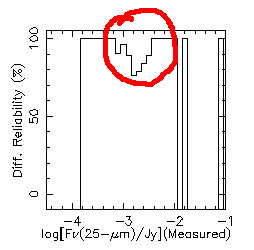
The notch in differential reliability... And it's cause - artifacting around bright point sources.


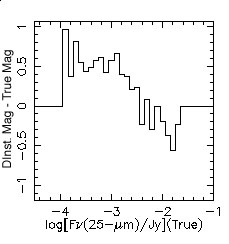
A more pressing concern is that the achieved resolution of R-L is flux- dependent, i.e. in the deconvolved image bright sources will have a higher achieved spatial resolution than faint ones. This is a feature of every deconvolution algorithm I can think of. However, the source extractor implicitly assumes that the PSF is flux-independent. As a result, it's extracted fluxes are wrong, except for sources similar in brightness to those used to make the PSF. This is immediately apparent in a graph of the instrumental magnitude offset as a function of true source brightness.

Difference between instrumental and true magnitude.
Because the shape of the PSF changes as a function
of source brightness, DAOPHOT under/overestimates
the source brightness.


As a result, it was necessary to ease the magnitude constraint when computing matches with the truthlist. In this case, the constraint was relaxed to 1.5 magnitudes (from the normal value of 0.75). Since at very low flux levels the true source areal density is very high, relaxing this constraint will produce many more random "false" matches at low flux levels since the probability of a source meeting the brightness criterion falling inside the search radius becomes high. To partially combat this, I tightened the matching radius (maximum distance between detected and true source) to 7" from the normal 12". This is justified since an examination of the radial position error indicates that the positional accuracy is usually on the order of a few arcseconds. In an attempt to quantify the number of "false matches" being made by the match program, I performed the following experiment. If the detected source list is actually being correctly matched to the true source list with no random matches, then scrambling the positions of the detected sources should result in all of them being rejected as false. I therefore took the detected source list and randomly assigned new positions to all of the objects fainter than 0.7 mJy, which I then attempted to rematch. Of the expected 177 new false sources, six were still marked as real. In the following figure, the red circles are the sources marked as real in the raw coadd, while the green are the additional 6.

Red sources are true matches detected in the raw coadd.
The green circles are new matches made after the original positions
were scrambled. In theory, no new matches should have
occurred - these six are the result of randomly matching sources
meeting our position and brightness constraints.


What exactly this means is as yet unclear to me. The six additional matches (around 3% of those correctly identified as false) have been randomly matched with real sources. If we define the reliability as the ratio of (true matches - random matches) to all detected sources, then the real cumulative reliability of the deconvolved image drops to around 93%. Most of the erroneous sources are quite faint, and hence the reliability hit is taken at flux levels near 0.1 mJy.

Here is a pdf file for a quick presentation I have thrown together.

3. CLEAN

CLEAN has been a favorite of radio astronomers for years. It is not really a deconvolution algorithm per se, but since it is not fourier-based it avoids some of the pitfalls of the other algorithms. I have chosen to use Bill Keel's SCLEAN algorithm. It works by finding the point of highest significance in the image (usually the brightest), and subtracting from it a scaled model of the PSF. This model is additionally scaled by a "damping factor" such that each iteration might subtract only 1/50 of the peak value (this is the primary difference between what CLEAN and DAOPHOT do). This process is iterated several thousand times. The resulting map of point sources is then convolved with a simple beam (such as a diffraction-limited gaussian) and then added back to the data to form the CLEANed image. The algorithm makes the implicit assumption that the data can be well-modeled by point sources, but that is precisely the case for WIRE.

Pipeline Coadder CLEANed Image Truth Image


Shown above is the result of 2500 iterations of the SCLEAN algorithm applied to a simulated coadd of 40 frames at 12um. The PSF was same as used above for the R-L deconvolution. Many features are now visible, and a visual comparison with the truth image at right indicates that nearly all of the CLEAN features do appear to correspond to real features.

The results of CLEAN processing have now been q uantified. They appear quite promising.